February 11th, 2025
Independent Samples T-Test Definition & Guide
By Connor Martin · 9 min read
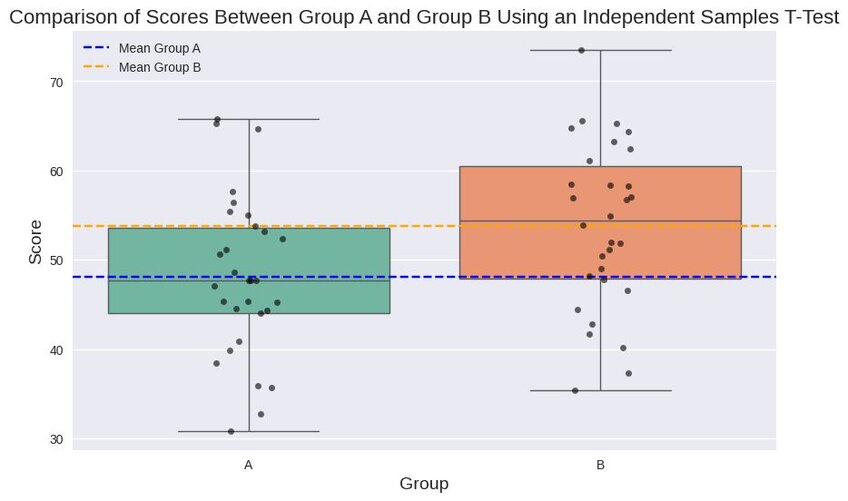
Also known as a two-sample t-test, the independent t-test is among the most common forms of statistical analysis.
It’s used in a wide range of industries. Healthcare, marketing, and education are just a few. All use the test to determine the same thing: what (if any) difference in mean exists between two independent datasets.
Key Takeaways
- The independent samples t-test compares the means of two unrelated groups to determine if a significant difference exists, with applications in fields like healthcare, education, and business.
- Key assumptions for validity include normality, homogeneity of variance, and group independence; violations may require alternative tests like ANOVA or the Mann-Whitney U-test.
- Statistical software simplifies the process, helping to check assumptions, calculate values (e.g., p-values), and interpret results for research or business decisions.
What Is an Independent Samples T-Test?
The independent samples t-test determines whether a significant difference exists between the means of two independent groups. For that determination, you need a pair of hypotheses that underpin your independent t-test:
- The null hypothesis: There’s no difference between the means of the two groups.
- The alternative hypothesis: There is a significant difference between the two sample means.
Either way, the groups must be different and contain entirely different participants. This means that the data from the two groups should not match at all.
Key Assumptions of an Independent Samples T-Test
An independent t-test cannot be performed on any random sample. The data used must meet specific assumptions, which are listed below.
Normality
The dependent variable should be approximately normally distributed within each group, which means the values should follow a bell-shaped curve with most data points near the mean and fewer at the extremes. Minor deviations are acceptable, especially with larger sample sizes.
Homogeneity of Variance
Homogeneity of variance means that the variability in scores should be similar for both groups. Significant differences in variability can skew the results, so this assumption is often tested using Levene’s test.
Independence
Your two groups should be entirely independent, meaning no participant should appear in both groups, and their data should not overlap.
Some good examples include male vs. female and employed vs. unemployed groups. The participants must also be independent, meaning that the two independent samples must not share any participants.
When to Use an Independent Samples T-Test
The independent samples t-test is used to compare the means of two unrelated groups, interventions, or scores. Here are some more specific examples of this comparison.
Practical Applications in Research and Business
The independent t-test is widely used in medical research and business. Two common practical applications explain why. In medicine, this test is often used to compare the effectiveness of a treatment in two independent groups. In business, it can determine whether two advertising campaigns generate the same sales.
Examples of Common Scenarios
The independent t-test is commonly used for the following scenarios:
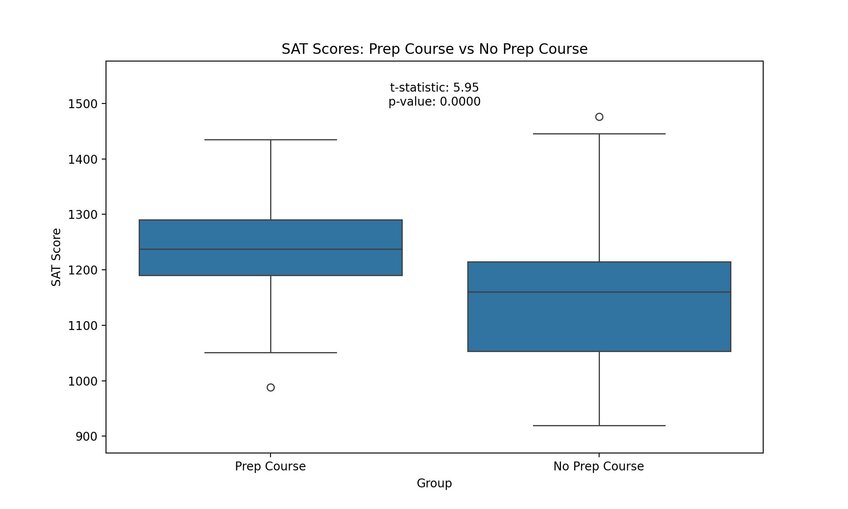
- Comparing SAT scores between students who took a prep course and those who didn’t (education)
- Assessing whether two production lines make items of the same quality (manufacturing)
- Investigating if job satisfaction levels differ between remote and in-office employees (social science)
How to Perform an Independent Samples T-Test in 4 Steps
Here’s a brief overview of the independent samples t-test.
Step 1 – Collect and Prepare Data
A statistical test always starts with collecting data. For this test, the data should come from two unrelated groups.
Step 2 – Check for Assumptions
Your data must meet all the necessary assumptions for this statistical test to produce valid results. That’s why you must check your data for assumptions before actually performing the independent t-test.
You can do so with statistical software like IBM SPSS Statistics. This software has a built-in Levene’s test, which checks the homogeneity of variance assumption.
However, you can also check some assumptions independently. For example, the Shapiro-Wilk test is an excellent test for normality. As for the independence assumption, it can sometimes be checked manually. You just need to make sure your two groups don’t overlap in participants or data.
Step 3 – Calculate the Test Statistic
You’ll need two values to successfully perform the independent t-test. The first is the test statistic. This value helps you understand how different the two groups are from each other.
The second value you’ll need – and get – is the p-value. Thanks to this value, you’ll know whether the difference between the two groups is statistically significant.
Step 4 – Interpret the Results
The calculated p-value will tell you whether to reject the null hypothesis or not. You can then use this knowledge for future decision-making.
Independent Samples T-Test Formula and Calculations
Here’s how you can go about actually calculating all the necessary values for the independent t-test.
Formula Breakdown
The independent t-test calculates the test statistic (t) using two formulas. The choice depends on whether equal variances are assumed.
If you assume equal variances, the formula will be as follows:
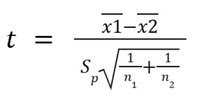
Here’s the breakdown of this formula:

If, however, you don’t assume the equal variances, you must use this formula:
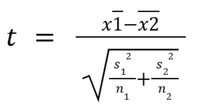
In this formula, the s1 is the standard deviation of the first sample and the s2 of the second.
Manual Calculation Example
Medical testing is where you’ll most often find independent t-tests being used.
Let’s go with a straightforward example – blood pressure. You have a new blood pressure-reducing medication you want to test. So, you’ll split a randomized group of people with high blood pressure into two groups.
First, you have the group you’re testing with the new medication, with the second group being a placebo set that either thinks it’s taking the new medication or is receiving conventional treatment. This gives you the two independent groups you need for your t-test.
You monitor the patients on medication for several months. After your study period concludes, you’ll have two sets of numbers: one covering the patients using your medication and the other the numbers of the placebo group.
From there, follow the steps and use the formula we’ve already discussed, and you will find the mean for each of these groups. In this example, you’re testing whether the mean blood pressure reduction of the medicated group is significantly different from that of the placebo group. If the p-value is less than 0.05, you can reject the null hypothesis and conclude there is a significant difference.
Using Statistical Software for Faster Results
Almost every part of the independent samples t-test can be manually calculated. However, this doesn’t mean you should take this approach. Using statistical software is much faster and more convenient. Plus, you can get accurate results even if statistics isn’t your strong suit.
Understanding and Interpreting Results
Once you – or the software – finish all the calculations, you’ll only see figures. If you don’t know how to interpret them, that’s all they’ll be – a group of numbers. Here’s how to convert them into useful information.
P-Values and Statistical Significance
The most commonly chosen statistical significance level is 0.05. If your p-value is less than this number, you can reject the null hypothesis. In other words, there’s strong enough evidence against this hypothesis. If, however, your p-value is greater than 0.05, the evidence against the hypothesis is lacking. As a result, you accept it.
Confidence Intervals and What They Mean
Confidence intervals give you an idea of the size of the difference, not just its significance. These intervals are displayed as a range of values in which the true mean difference might lie.
You’ll also see them used with percentages. For instance, a 90% confidence interval means that if you were to repeat the study 100 times, 90 of them would contain the true mean difference.
Reporting Results in Research or Business Reports
In professional surroundings, you should report results in APA style. This style has a few strict rules to follow:
- You must list the t-statistic with two decimal places.
- You must calculate the degrees of freedom. The formula is n1 + n2 – 2.
- The exact p-value should only be reported if it’s not significant. If it is, you can report it as p < 0.05.
Limitations of an Independent Samples T-Test
The independent samples t-test is an invaluable statistical tool in many scenarios. Many, but not all. Here are the limitations of this test.
When the Test May Not Be Appropriate
The independent t-test isn’t appropriate in the following scenarios:
- There are significant outliers (which can distort results and violate the assumptions of normality and homogeneity of variance).
- You want to compare more than two groups.
- Your data violates any of the key assumptions.
Alternatives to Consider
If the independent t-test isn’t appropriate for your data, you can take two approaches – transforming your data or using another statistical test altogether. Consider ANOVA for comparing three or more groups or the Mann-Whitney U-test for non-normal data, as both are strong alternatives to the independent t-test.
Try Julius Today to See How Easy and Straightforward Statistical Analysis Can Be
Even with all the statistical tools at your disposal, performing the independent samples t-test can be rather challenging. That’s why you need an AI-powered helper. Julius AI makes any statistical analysis – including the independent t-test – quick and easy.
Frequently Asked Questions (FAQs)
What is an independent t-test used for?
An independent t-test is used to compare the means of two unrelated groups to determine whether a significant difference exists between them. It is widely applied in research fields like healthcare, education, and business to analyze group-level differences.
What is the difference between dependent and independent t-tests?
The primary difference lies in the relationship between the groups being compared. An independent t-test compares two unrelated groups, while a dependent t-test, also called a paired t-test, compares means from the same group measured at two different times or under two conditions.
What is the difference between paired t-tests and independent t-tests?
A paired t-test evaluates the mean difference within the same group (e.g., pre-test vs. post-test scores), whereas an independent t-test compares means between two entirely separate groups. The paired t-test accounts for the inherent connection between measurements, while the independent t-test assumes no overlap between datasets.
In which cases would an independent sample t-test not be appropriate?
An independent t-test is not appropriate when the data violates key assumptions like normality, independence, or homogeneity of variance. It’s also unsuitable for comparing more than two groups or when significant outliers distort the results, requiring alternative tests like ANOVA or the Mann-Whitney U-test.
